Hello, Geo-fence! - 우아한형제들 기술 블로그

안녕하세요 라이더스개발팀 박민철 입니다.
BROS(Baemin Riders Operating System)에 Geo-fence를 도입한 경험을 적어보겠습니다.
(BROS는 라이더를 배차하고 음식을 픽업하여 고객에게 전달하는 서비스를 지원하는 배달 플랫폼 입니다.)

Geo-fence란?

‘geo-fencing’ 으로 불리기도 하는데, 지도위에 가상의 도형들의 영역을 말합니다.

[이런식으로 그리면 혼나요]

근데 왜 필요한거죠?

기존에는 지점(관제센터)의 행정동코드 기반으로 배달 가능 여부를 판단하였습니다.
고객의 행정동코드와 지점의 배달 가능한 행정동코드를 매핑하여, 배달 가능한 지점이 존재하면 주문을 생성할 수 있었습니다.

여기에서 1가지 같은 2개의 이슈가 발생합니다.

[경계선 주변 배달불가능] 첫 번째는 고객이 배달 가능 지역에 가까워도 특정 지점의 행정동코드가 없으면, 배달할 수 없는 문제입니다. 경계선 근처에 거주하는 고객에게 서비스를 제공하지 못한 안타까움이 있습니다.

[움직일 기미가 안 보이는 라이더님] 두 번째는 배달 가능 지역내 일부 영역을 제외할 수 없는 문제입니다.
이 프로젝트가 진행되어야 하는 이유의 많은 지분을 차지하고 있습니다. 공원이나 오토바이가 진입하기 어려운 지역, 오랜 시간을 소요해야 하는 지역(타*팰리스는 보안 때문에 출입시간 소요가 많습니다.)을 피크타임에 유연하게 처리할 수 있도록 해야 합니다.

그래서 어떻게 했는데요?

먼저 Geo-fence를 사용하기 위해 네이버 지도 API 문서를 잘 읽었습니다.
그다음 BROS에서 지점별로 접수영역과 차단영역을 그리고 저장할 수 있도록 기능을 개발했습니다. 그리고 행정동코드기반 로직에 접수영역과 차단영역을 추가로 판단하여 배달 가능 여부를 전달하도록 수정하였습니다.

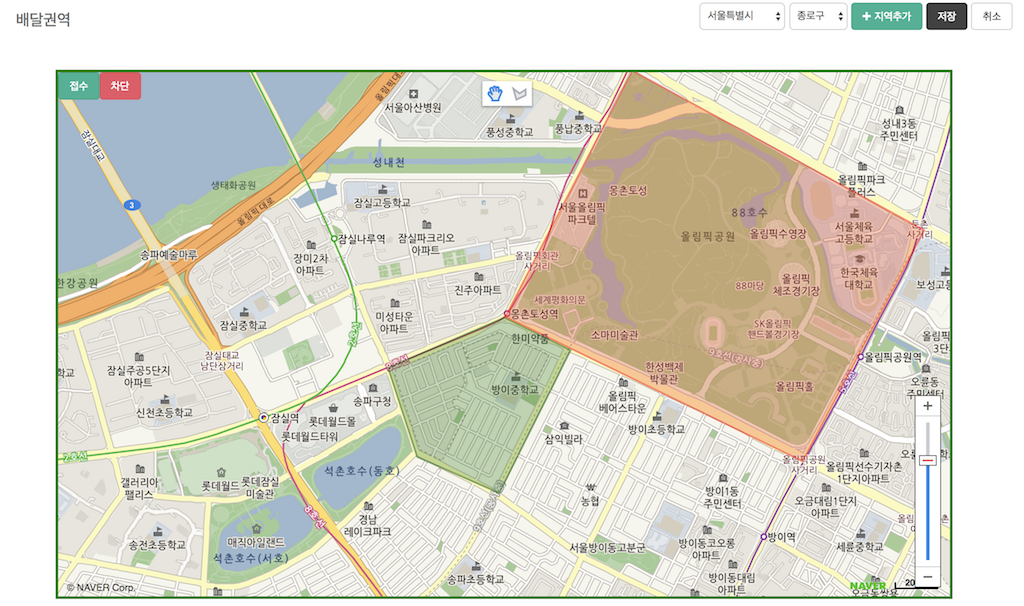[접수영역과 차단영역을 그려봅니다]

약간의 문제가 있습니다.

기존 시스템에서는 지점들의 배달 가능한 행정동코드를 On/Off로 관리하고 있었습니다.
관리자가 접수영역과 차단영역을 적절하게 그릴 수 있도록 행정동의 정보를 Geo-fence로 같이 볼 수 있어야 했습니다.

그래서 통계청 통계지리정보서비스에서 제공하는 행정동 경계 파일을 기반으로 작성된 geojson 파일을 사용하여 행정동 영역을 저장하였습니다. ( github에 공유해주신 개발자님 감사합니다. )

하지만, 통계지리정보서비스에서 제공하는 코드는 7자리 행정구역분류코드이고, 저희가 사용하는 코드는 10자리 행정표준코드관리시스템코드이기 때문에 변환이 필요했습니다. ( 아 … 할많하않 )
통계분류 포털 홈페이지의 행정구역분류 엑셀 데이터를 다운받아 매핑을 할 수 있었습니다.
(이 삽질작업은 오픈 프로젝트인 우아한주소에 저장되어 있습니다.)

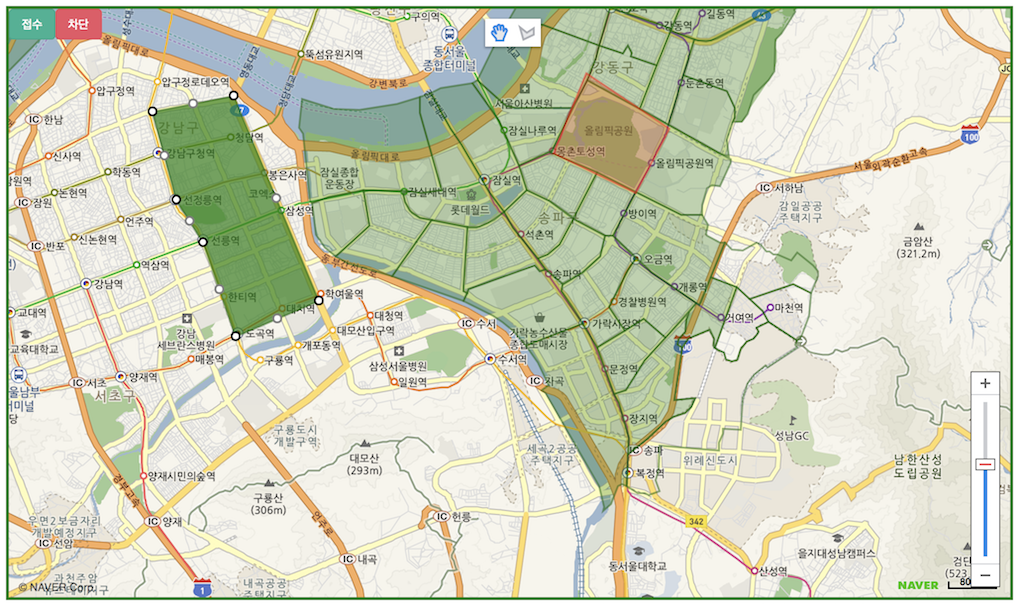[행정동과 같이 접수영역과 차단영역을 그려봅니다]

마지막으로 로직을 수정합니다.

기존 로직에 행정동코드 포함 여부에 추가로 고객의 위치가 접수영역 안에 있는지 혹시 차단영역 안에 있는지 판단하는 기능을 추가하였습니다. 이렇게 간단하진 않지만, 대략 이런 느낌입니다.

...
boolean deliverable = ((행정동코드포함 || 접수영역안에위치함) && 차단영역안에없음);
...

끝.

더 들여다봅시다.

~~바쁘신 분들은 뒤로가기를 눌러주세요.~~

Geo-fence에서 생성한 도형 안에 점(Point)이 존재하는 여부를 JTS(평면 기하학을 위한 기능을 제공하는 오픈소스 Java 라이브러리)를 사용했습니다. Point.class와 Polygon.class은 Geometry.class를 상속받아 사용하고 있었으며, 적절해 보이는 within이라는 함수를 사용했습니다.

한번 테스트를 해봅니다.

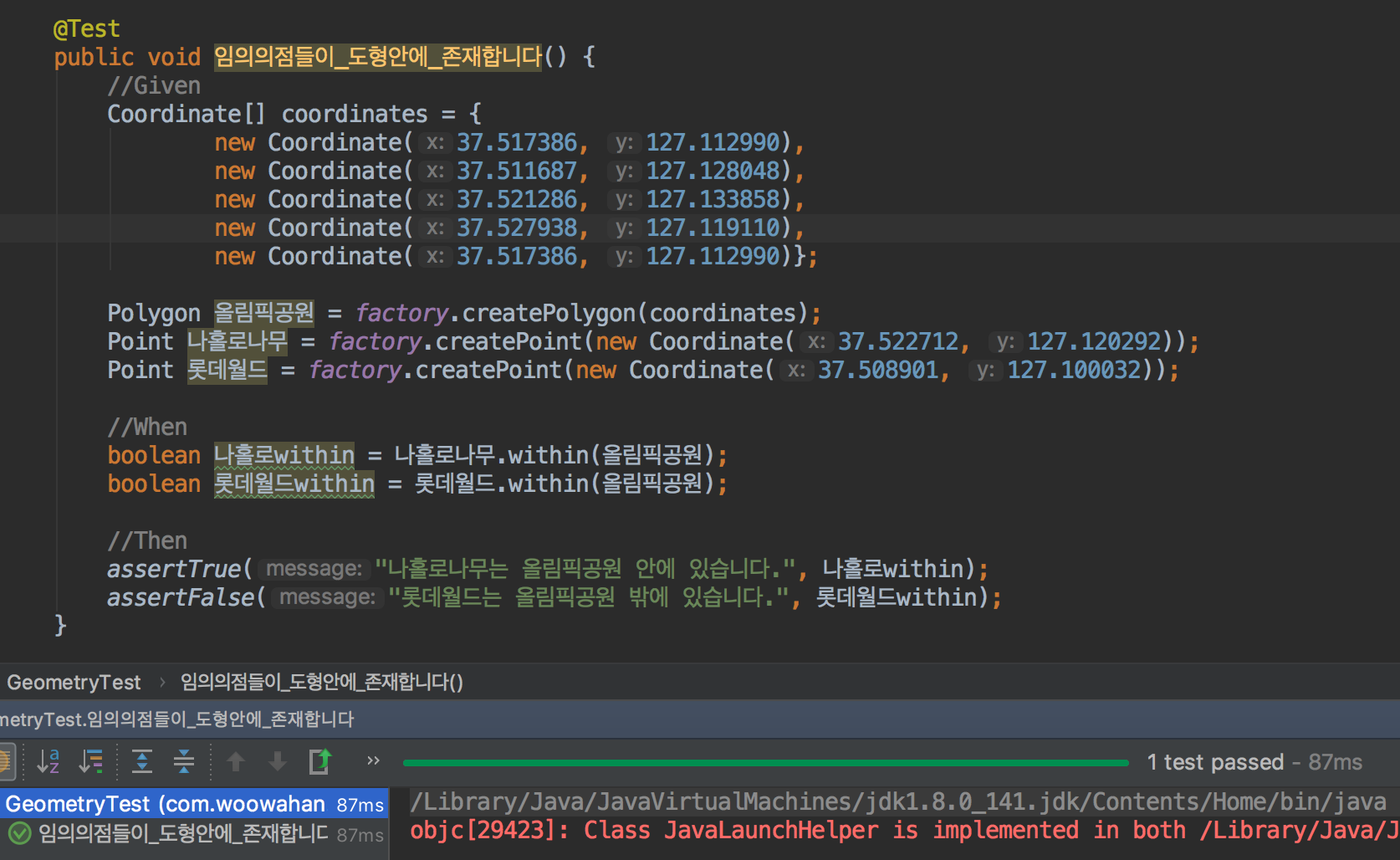[테스트통과는 언제나 기분이 좋아요]

궁금증이 하나 생깁니다. 영역의 경계선 위에 점(Point)이 있으면 어떨까요? 제대로 동작할까요?

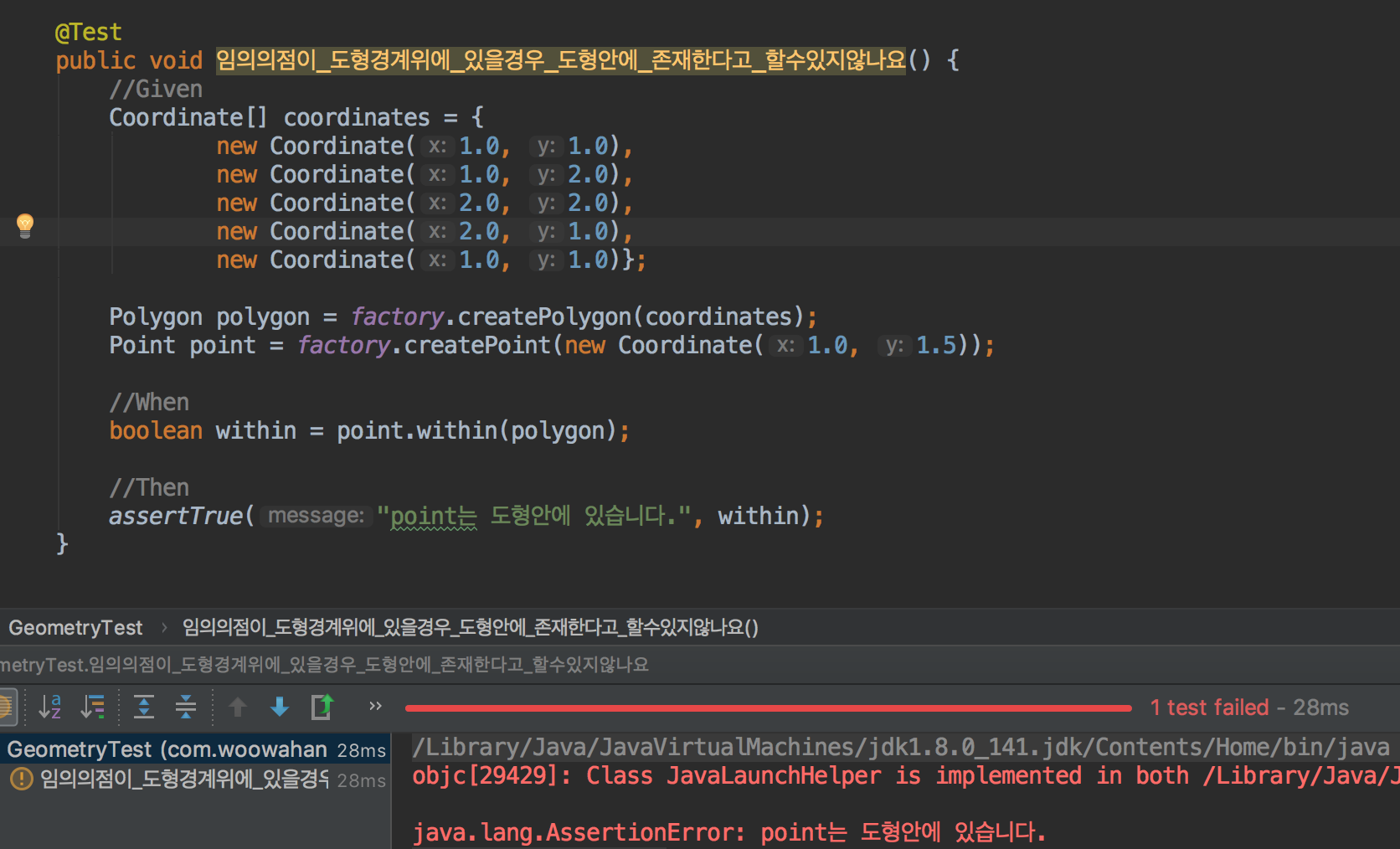
점(Point)이 영역의 경계선에 있으면, 안에 있다고 판단하지 않습니다. 그렇군요.
문서를 읽어봅시다. (영어라서 문서를 먼저 안 읽…)

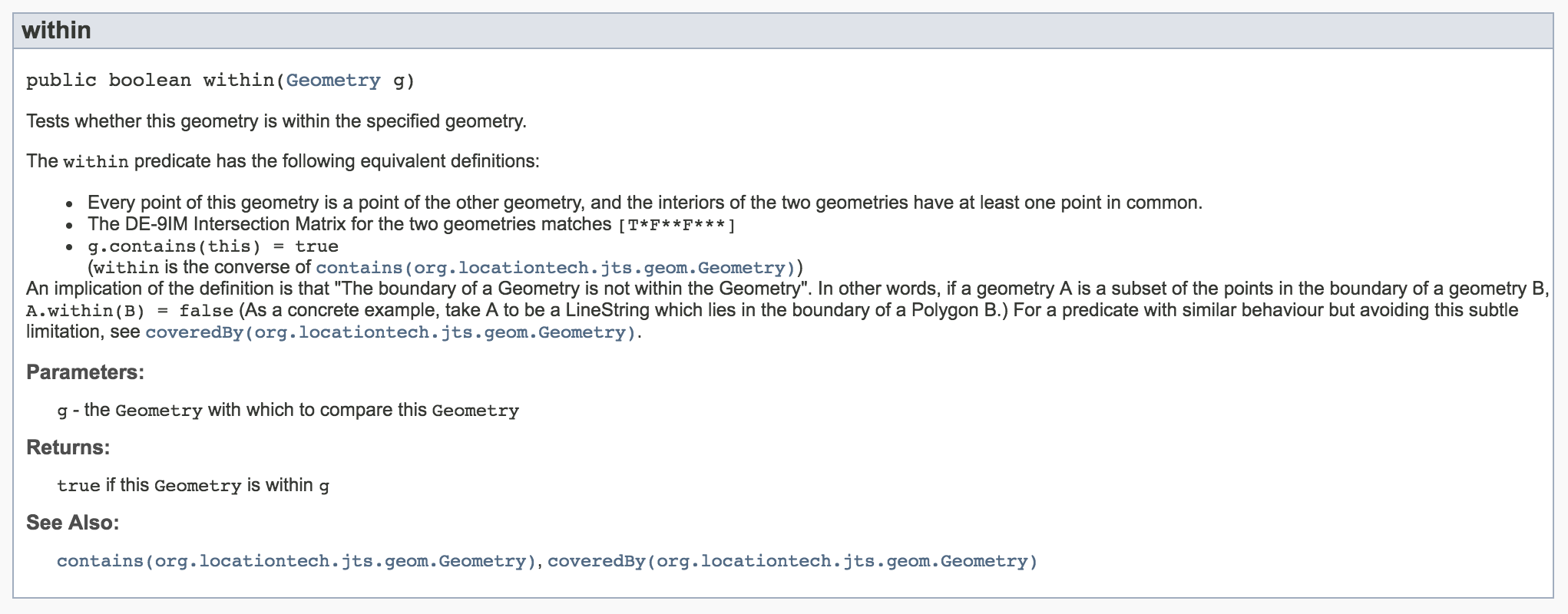문서를 보면 contains, covers, coveredBy, equals … 그럴듯한 함수들이 있습니다.
앞서 사용한 within 함수를 살펴보면 DE-9IM 단어와, [T * F * * F * * * ] 표기가 있습니다.
잘 모르겠습니다. 그래서 검색을 해봤습니다.

DE-9IM?

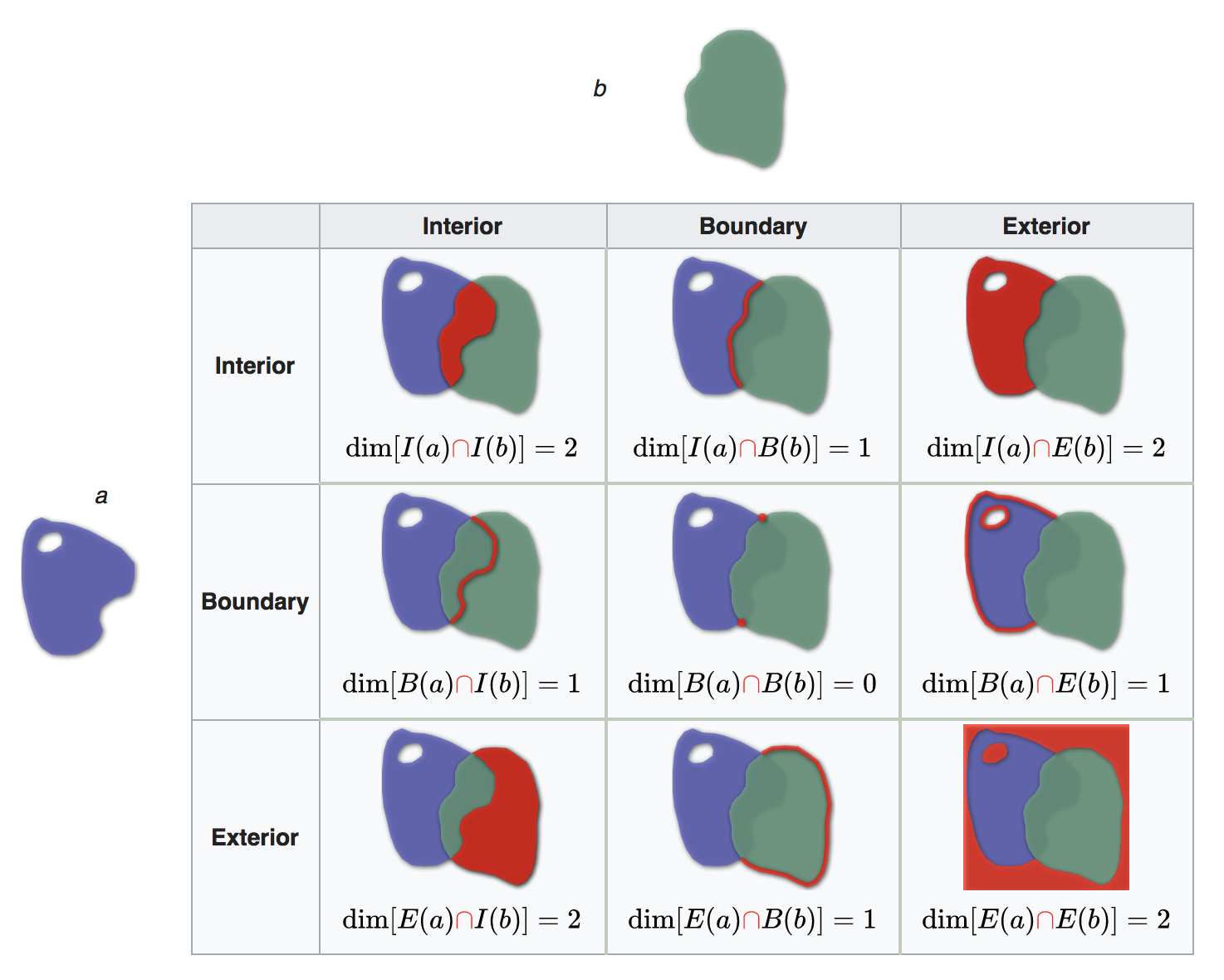[DE-9IM : 두 도형의 관계를 행렬로 표현해 봅시다]

DE-9IM은 두 도형의 내부, 경계, 외부의 총 9가지의 관계를 표현하며, 교집합에서 발생하는 도형의 Dimension(차원)을 행렬로 나타냅니다. 그림에서 보면 II(가장 왼쪽 위)는 교집합의 도형이 2차원이기 때문에 2가 나오고, IB는 교집합이 직선이므로 1이란 값이 도출됩니다.

A simplified version of dim(x) values are obtained mapping the values {0,1,2} to T (true),
so using the boolean domain {T,F}.

종류	Dimension	boolean
점(Point)	0	T
선	1	T
면	2	T
EMTPY	-1	F

[Dimension이 0이라고 false가 아닙니다!]

그리고 DE-9IM을 boolean으로 변환할 때 점, 선, 면은 모두 true이며 존재하지 않는 도형은 false가 됩니다.
그럼 다시, 앞서 작성한 두 가지의 테스트코드를 다시 살펴봅시다.

테스트를 통과하지 못한 이유

앞에 두 가지의 경우에 대해 테스트코드를 작성했습니다.

점A가 영역B 안에 있는 경우
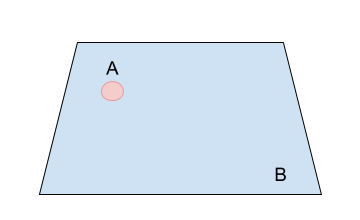DE-9IM(A, B) = [0 F F F F F 2 1 2]
점A가 영역B 경계선에 있는 경우
DE-9IM(A, B) = [F 0 F F F F 2 1 2]

문서에 보면 within을 포함한 covers, contains … 함수들의 DE-9IM 규칙을 설명한 내용이 있습니다.

within의 규칙은 [T * F * * F * * *]입니다. 그래서 1번 조건은 만족하지만, 2번 조건을 만족하지 않습니다.
그래서 테스트코드에서 within의 값은 false로 반환됨을 알 수 있습니다.

2번 조건을 만족하기 위해선 wihtin 함수가 아니라 coveredBy 함수를 사용해야 합니다. contains는 within의 도형의 순서가 바뀐 것이며, covers와 coveredBy도 유사한 관계를 알았습니다.
역시 아는 만큼 보입니다!

문서를 잘 읽고 개발을 합시다.

끝.

조금 더 들여다봅시다.

~~수포자들은 뒤로가기를 눌러주세요~~

DE-9IM을 사용하여 두 도형의 관계를 표현하는 방식을 알았습니다.
그런데 말입니다.
두 도형의 교집합을 판단하는 건 어디까지나 저의 뇌피셜로 판단을 했는데요, 한 점(Point)이 다른 도형 안에 있다는 것을 어떻게 컴퓨터가 판단하는지 궁금해졌습니다. 그래서 한번 찾아봤습니다.

보통 가장 많이 사용하는 방법은 Ray Casting Algorithm입니다.

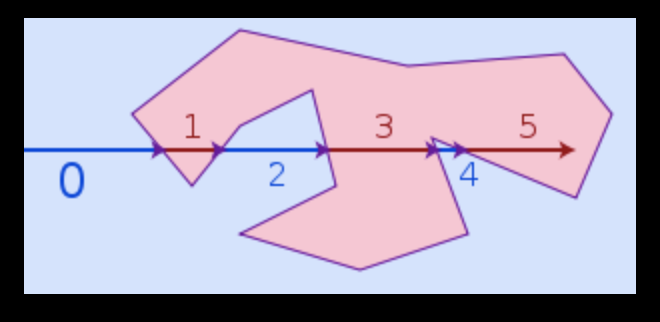[알고리즘이라서 그런지 0부터 시작(소오름)]

알고리즘은 대략 이렇습니다. 그림을 보면 알 수 있듯이, 점을 지나는 임의의 직선을 하나 쭉! 그립니다. 그러면, 그 직선과 도형이 만나는 교점이 생깁니다. 이 교점을 기준으로 7개의 선이 만들어집니다. 그 점이 홀수 번째 선 위에 있으면 도형 안에 포함, 짝수 번째 선 위에 있으면 도형 밖에 있다고 판단하면 됩니다. ( 이렇게 심플한 방법이! )
그럼 만만한 문제를 한번 풀어봅시다.

수학적 사고를 언어로 작성합니다.

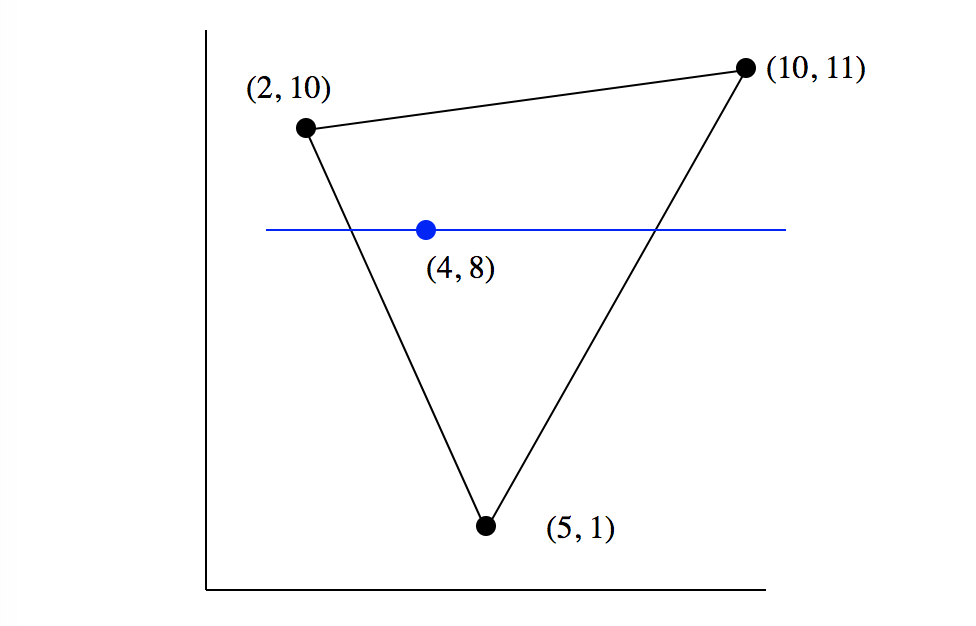[수학문제 같이 생긴 문제를 풀어봅시다]

임의의 점(4, 8)이 삼각형 안에 있는지 밖에 있는지 확인하시오. (3점)
문제를 해결하는 순서는 다음과 같습니다.

삼각형 직선 3개 방정식을 구한다.
점(4, 8)을 지나는 직선(y = 8)과 직선 3개의 교점을 구한다.
점(4, 8)이 교점들 사이 몇 번째 선위에 있는지 구한다.
작성 후 자신의 노력에 감동하여 오열한다.

먼저 좌표들을 순회하면서 직선의 방정식을 구합니다.

Coordinate[] coordinates = {
            new Coordinate(2.0, 10.0),
            new Coordinate(10.0, 11.0),
            new Coordinate(5.0, 1.0),
            new Coordinate(2.0, 10.0)};

for (int i = 0; i < coordinates.length - 1; i++) {
    Coordinate curr = coordinates[i];
    Coordinate next = coordinates[i + 1];

직선의 방정식

직선의 방정식은 y = ax + b ( a는 기울기, b는 y절편 ) 입니다.
두 점이 있는 경우 기울기( y증가량 / x증가량 )를 구하고, y절편은 두 점 중 한 점과 기울기를 대입하여 값을 구합니다.

    Double angle = (next.y - curr.y) / (next.x - curr.x);
    Double yIntercept = curr.y - (angle * curr.x);

3개의 직선 방정식을 구했습니다. 이제 직선들과 점(4, 8)을 지나는 파란 직선(y = 8)과의 교점을 구합니다.
y = angle * x + yIntercept 직선에 y = 8을 대입하여 교점(?, 8)들의 x좌표를 구합니다.

    Double xIntersection = (8 - yIntercept) / angle;

교점

교점을 모두 구하면, 다음과 같이 3개의 교점(빨간색점)의 x값을 찾을 수 있습니다. 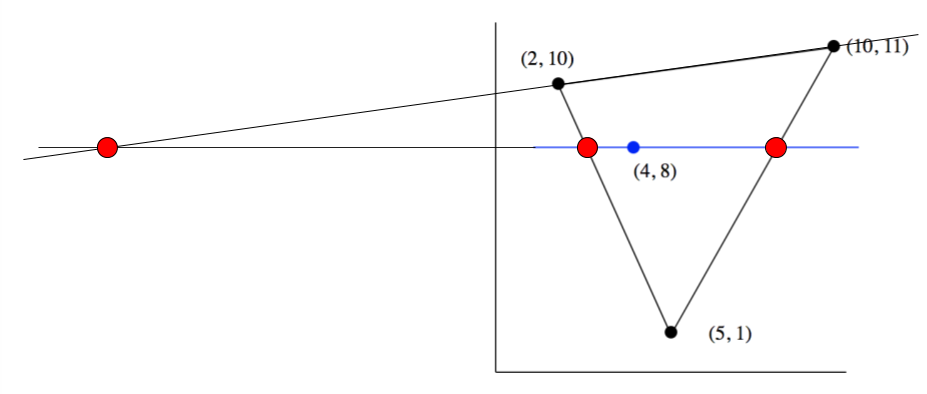[예외인 녀석이 있는 것 같다]

그림에서 보면 가장 왼쪽에 있는 교점(빨간색점)은 삼각형의 변 위의 점이 아니기 때문에 예외를 해줘야 합니다.
두 점의 x 값을 범위로 지정하여 교점이 그 사이에 있는지 판단하고, 삼각형과 만나는 교점만을 리스트에 추가합니다.

    // 두 점의 중간값과 차이를 구하고 교점이 사이에 있음을 판단합니다.
    Double middle = (curr.x + next.x) / 2;
    Double distance = Math.abs(next.x - middle);
    boolean between = Math.abs(xIntersection - middle) <= distance;
    if (between) {
        xIntersections.add(xIntersection);
    }

몇 번째 선 위에 있는가?

마지막으로, 점(4, 8)이 교점들 사이에 생긴 선 중 몇 번째 속하는지 판단합니다.

    int x = 4;
    // 간단한 계산을 위해 최대값과 최소값을 넣어줍니다. 
    xIntersections.add(Double.MAX_VALUE); // +무한
    xIntersections.add(Double.MIN_VALUE); // -무한
    xIntersections.sort(Double::compareTo);
    ...
    for (int i = 0; i < xIntersections.size() - 1; i++) {
        Double curr = intersections.get(i);
        Double next = intersections.get(i + 1);
        if (curr < x && x < next) {
            // 짝수 번째는 OUT, 홀수 번째는 IN. 
            boolean within = (i % 2 == 1);
            return within;
        }
        ...
    }
    ...

감동적인 마무리

수고하셨습니다. 드디어 끝났어요! ( 짝짝짝 )
이렇게 간단(?)하게 작성할 수 있었습니다. 하지만 현실은 그렇게 간단하지 않죠.
알고리즘이 매력적으로 간단하지만, 항상 잘 작동하는 것은 아닙니다.

Unfortunately, this method won’t work if the point is on the edge of the polygon.

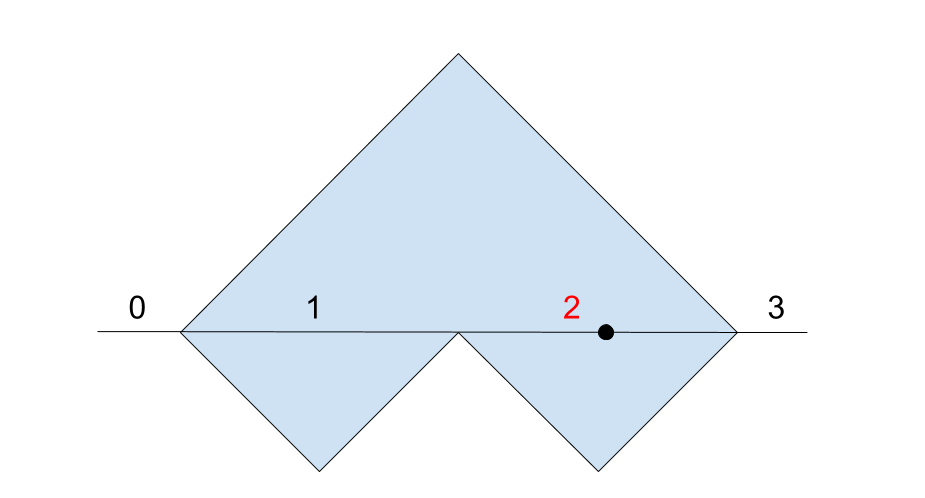
이런 경우는 임의의 점이 도형 안에 포함되어 있지만, 알고리즘에 의하면 짝수 번째의 선 위에 있어 밖에 있다고 잘못된 값을 반환하게 됩니다. 물론 현실에서 사용하는 도형들은 유한한 점으로 표현하기 때문에 충분히 예외를 처리할 수 있습니다.

끝맺으며

포스팅을 간단하게 시작했지만, 내용이 산으로 가기도 하고, 기술과 멀어지고, 많이 길어지기도 했습니다. 이런 글도 있어야 다양한 곳에서 인사이트를 얻을 수 있다는 핑계로 작성을 했습니다. 개인적으로, 오래전부터 지도 API를 사용하면서 폴리곤 같은 도형 안에 포함 여부를 판단하는 로직에 궁금증이 있었습니다. 우연한 기회에 잊고 있던 작은 호기심을 깊게 찾아볼 수 있던 좋은 경험이었습니다.
긴 글 읽어주셔서 감사합니다.

#문서를잘읽습니다 #영어공부필수 #일을이렇게열심히

진짜 끝.

참조문서