들어가며

안녕하세요.

우아한형제들 데이터서비스팀에서 섹시미 막내를 맡고 있는 김세환입니다.

데이터를 보다보면 예측모델을 만들게 되는 경우가 많은데요, 대부분의 경우 모델을 만들기 위한 함수들이 라이브러리 형태로 구현이 되어있다보니, 이런 라이브러리를 가져다 쓰는 것이 일반적입니다. 이 때문에 모델을 만드는 데 있어 그 내용은 놓치고 지나가기 쉽습니다.

이 포스트에서는 Linear Regression(선형회귀)를 파이썬으로 직접 풀어보고 내용을 한번 되짚어보며, 데이터를 통해 어떤 식으로 값을 예측을 할 수 있을지 간단하게 알아보려고 합니다.

배달시간이 얼마나 걸릴까…

다음과 같은 데이터가 있다고 해 봅시다.

# 배달거리, 배달시간 
[100m, 20min] 
[150m, 24min]
[300m, 36min]
[400m, 47min]
[130m, 22min]
[240m, 32min]
[350m, 47min]
[200m, 42min]
[100m, 21min]
[110m, 21min]
[190m, 30min]
[120m, 25min]
[130m, 18min]
[270m, 38min]
[255m, 28min]

각 배달건에 대해 배달거리와 배달시간을 기록해 둔 데이터인 듯 합니다.

이 데이터를 보면 딱히 계산을 하지 않더라도, “200m정도 떨어진 곳에서 배달시키려고 하는데, 몇 분정도 걸릴까?” 라는 질문에 “음… 30-40분 정도 걸릴 것 같은데?” 라고 말할 수 있을 겁니다.

아마 100미터 거리가 20분, 150미터가 24분, 240미터가 32분… 과 같이 거리가 증가함에 따라 시간도 비슷한 속도로 증가하고 있는 패턴을 보이기 때문일겁니다.

데이터를 시각화 해보면 그런 패턴이 한 눈에 보입니다.

import numpy as np 
from matplotlib import pyplot as plt 

data = np.array([[100, 20], 
		[150, 24], 
		[300, 36], 
		[400, 47], 
		[130, 22], 
		[240, 32],
		[350, 47], 
		[200, 42], 
		[100, 21], 
		[110, 21], 
		[190, 30], 
		[120, 25], 
		[130, 18], 
		[270, 38], 
		[255, 28]])

plt.scatter(data[:, 0], data[:, 1]) 
plt.title("Time / Distance")
plt.xlabel("Delivery Distance (meter)")
plt.ylabel("Time Consumed (minute)")
plt.axis([0, 420, 0, 50])
plt.show()

[파이썬 Matplotlib을 사용하면 쉽게 그래프를 그려볼 수 있다.]

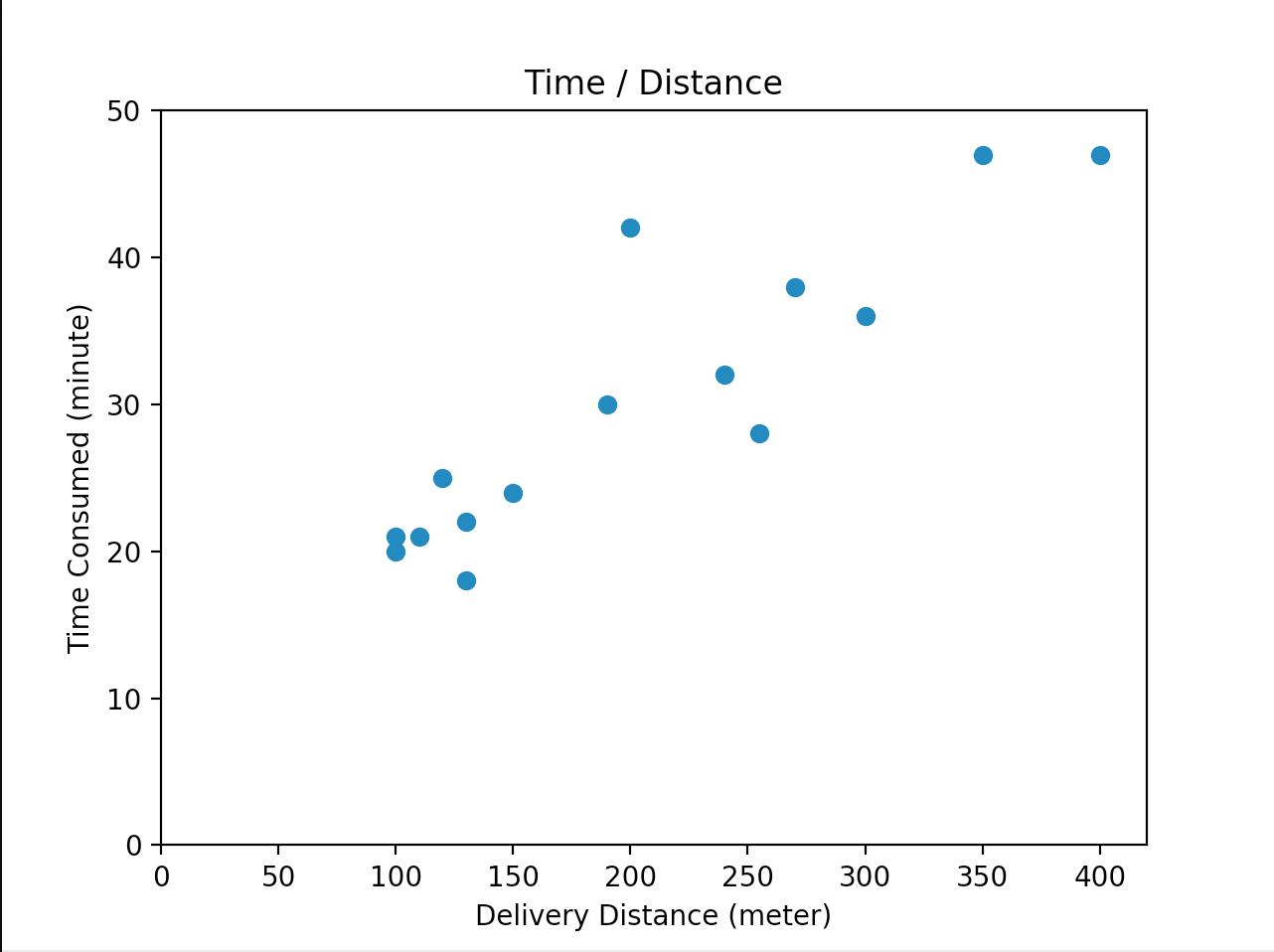
명확하지는 않지만 어느정도 패턴이 보입니다. 거리가 늘어남에 따라 시간도 비슷한 속도로 늘어나는 것을 볼 수 있습니다.

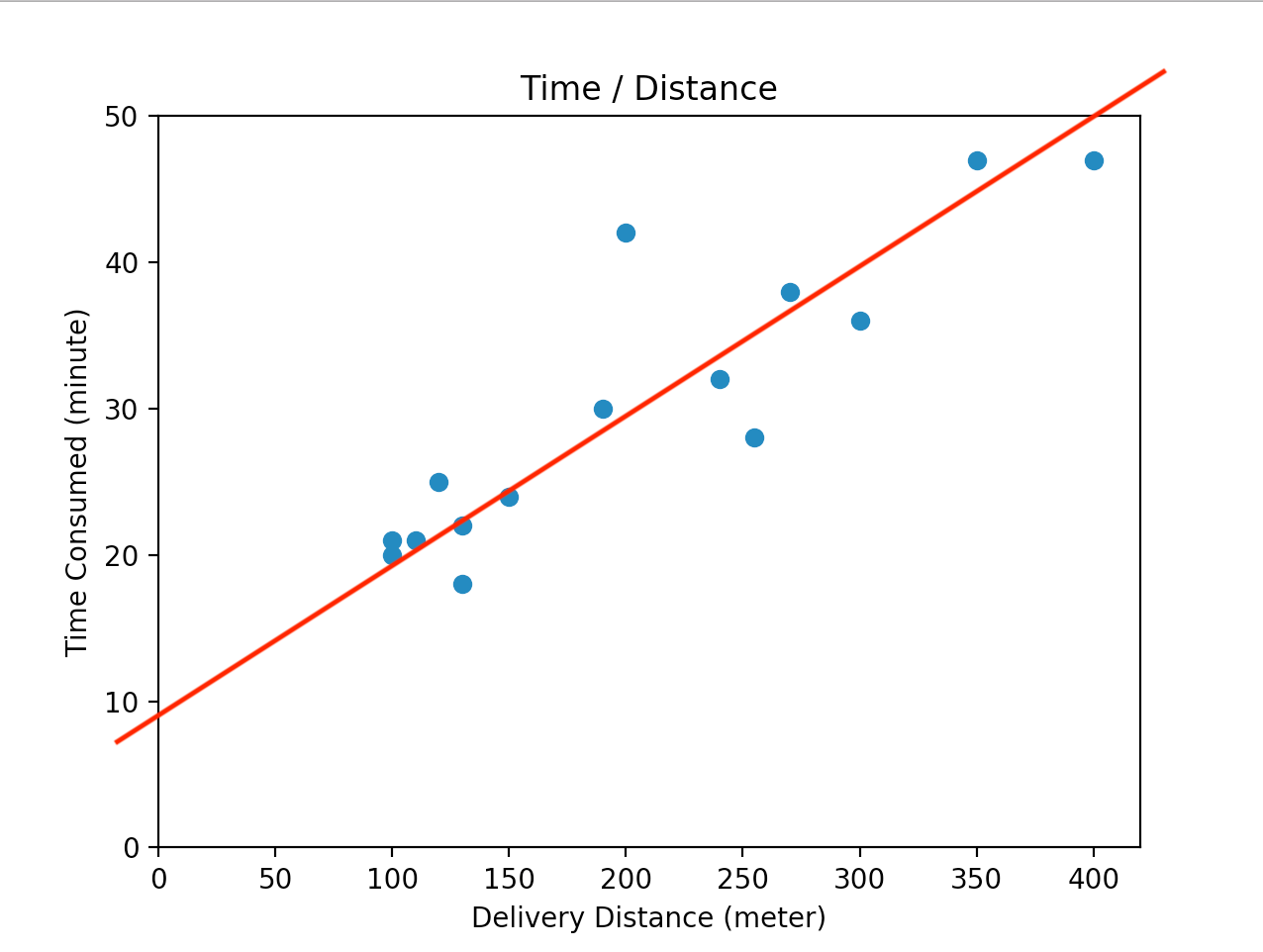[대에충 빨간 선 느낌]

대에충 이런 느낌이면 50m거리에서는 13? 14분정도 걸린다고 예상할 수 있을 것 같습니다. 200m면 30분정도면 배달이 될 것 같네요.

오늘 문제는 이런 선형패턴을 찾는 문제입니다. 이런 패턴을 찾으면, 다음에 배달이 있을 때 어느정도 시간이 걸릴지 예측해보는데 도움이 될겁니다. (맞을지 틀릴지는 모르지만요…)

하지만 (대~충 그려보는 것 말고) 선형패턴을 찾으려면 어떻게 하는게 좋을까요?

오차가 최소가 되는 선을 찾기

위 예제에서 볼 수 있는 것 처럼 데이터의 패턴을 비슷~하게 따라가는 선을 그을 수는 있지만 모든 점 위를 지나가는 하나의 선은 그을 수는 없습니다. 따라서 예측 값과 실제 값 사이에서 차이가 발생하게 됩니다.

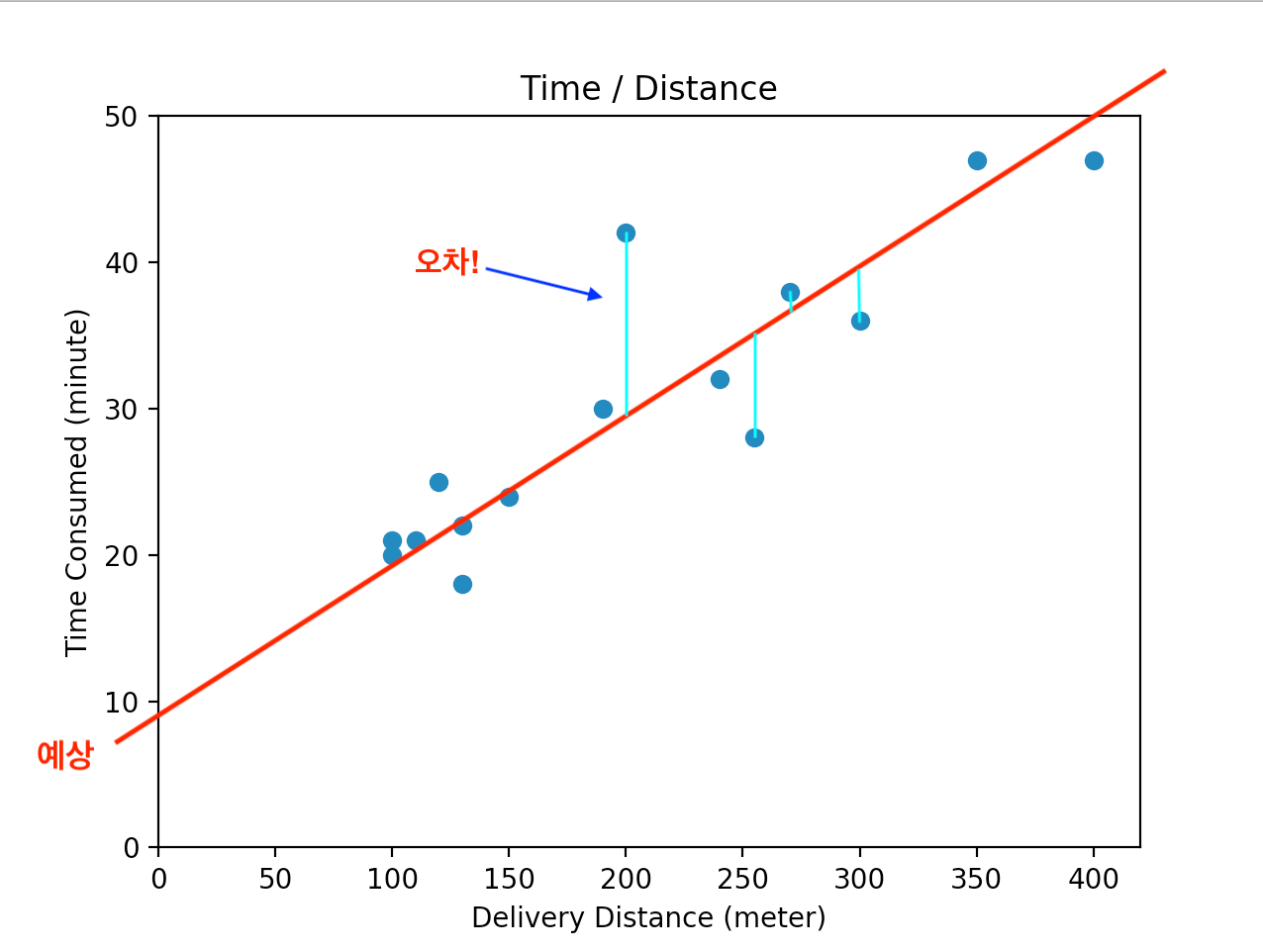[점이 선에서 멀수록 오차가 큰 것]

이 오차의 합을 최소한으로 줄이는 선을 찾는다면 예측을 가장 실제와 가깝게 하는 모델이라고도 할 수 있을 것 같습니다. (실제로는 데이터에 따라 더 여러가지 기준이 있을 수 있습니다.)

저희의 목표는 저 선과 점들의 거리의 합을 최소화 하는 것이기 때문에 +, -가 있는 오차의 합보다는 오차 제곱의 합을 구하는 것이 더 바람직해보입니다.

이제 저희의 목표는 오차 제곱의 합이 최소화 되는 선을 찾는 것입니다. [Linear Least Squares]

행렬로 문제를 표현해보기

사실 이런 선을 찾는 것은 배달거리 x와 배달시간 y 사이에 선형함수 $y = ax + b$가 있다고 생각하고 그 함수를 구하는 일입니다.

만약 그런 함수 $f$가 있다면, 다음과 같은 식들을 만들 수 있을 겁니다.

\[100a + b = 20 \\ 150a + b = 24 \\ 300a + b = 36 \\ ...\]

가진 배달데이터의 개수만큼 식을 가진 연립방정식이 나옵니다. 연립방정식은 행렬로도 표현할 수 있습니다.

\[Ax \cong b \hspace{10mm} \text{where} \hspace{10mm} A = \begin{bmatrix} 100 & 1\\ 150 & 1\\ 300 & 1\\ ... \end{bmatrix}, x = \begin{bmatrix} x_1 \\ x_0 \end{bmatrix}, b = \begin{bmatrix} 20 \\ 24 \\ 36 \\ ... \end{bmatrix}\]

하지만 변수가 2개인데에 반해 식이 너무 많아서, $Ax = b$를 만족하는 $x$를 찾을 수는 없습니다. 그래서 같음을 의미하는 $=$ 를 쓰지 못하고 $\cong$를 썼습니다. 대신에 $Ax - b$를 최소화하는 $x$를 찾아야합니다. 위에서 그래프로 보았던 것 처럼요.

그럼 이제 이걸 풀어야 하는데… 이걸 어떻게 풀죠?

잠시 다른 얘기

A-1) Orthogonal Matrix (직교행렬)

행렬 중 다음과 같은 특징을 가지는 행렬을 Orthogonal Matrix(직교행렬)이라고 부릅니다.

\[Q^TQ = QQ^T = I\]

T는 transpose(전치)를 나타내는 기호로, 열과 행을 교환해서 새로운 행렬을 얻는 연산입니다. 예를 들어 이런 식입니다.

\[A = \begin{bmatrix} 100 && 1 \\ 150 && 1 \\ 300 && 1 \\ ... \end{bmatrix} , A^T = \begin{bmatrix} 100 && 150 && 300 && ... \\ 1 && 1 && 1 && ... \end{bmatrix}\]

대각선 방향으로 스윽 돌리기만 하는거에요.

행렬 $I$는 Indentity Matrix(단위행렬)로 대각선이 모두 1이고 나머지는 0인 행렬을 말합니다.

\[I_n = \begin{bmatrix} 1& 0 & 0 & &0 \\ 0& 1& 0& ... & 0\\ 0& 0 & 1& &0 \\ & ... & & ... & \\ 0& 0 & 0 & & 1 \end{bmatrix}\]

이 Orthogonal Matrix가 가지는 특징 중 하나가 바로

\[\left\|Qv\right\|^2_2 = (Qv)^T(Qv) = v^TQ^TQv = v^Tv = \left\|v\right\|^2_2\]

$Qv$의 크기(norm)는 $v$의 크기와 같다는 것인데요, $Q$를 임의의 백터에 곱해도 그 크기에는 영향을 주지 않는다는 것을 의미합니다.

자세한 설명은 생략합니다. 이런 특성은 우리의 문제를 해결할 때 유용하게 쓰이니 기억해둡시다.

A-2) A가 Upper Triangular Matrix(상삼각행렬)이면 문제를 풀기 쉽다.

아까 위에서 식을 다음과 같이 만들었습니다.

\[Ax \cong b\]

그리고 $\left|Ax - b\right|$가 가장 작아지는 x를 찾는 것이 목표였죠.

만약 여기서, $A$가 Upper Triangular Matrix면 문제를 풀기 간단해집니다.

\[A= \begin{bmatrix} * & *\\ 0 & *\\ 0 & 0 \\ 0 & 0\\ 0 & 0 \end{bmatrix}\]

[Upper Triangular Matrix는 위 삼각형이 숫자, 아래 삼각형이 모두 0인 행렬을 말한다.]

이런 경우 식을 위(숫자가 있는 부분), 아래(전부 0인 부분) 두개로 나누어서 생각할 수 있습니다.

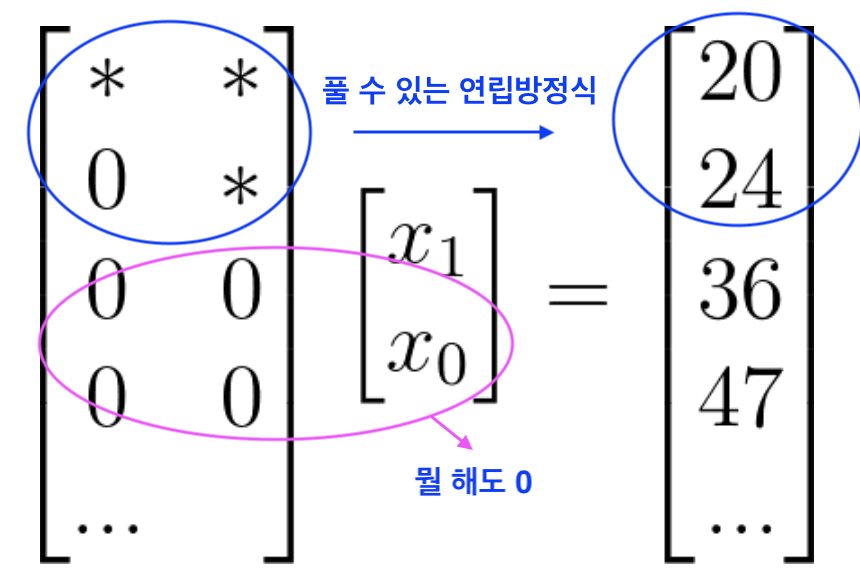위 숫자가 있는 삼각형으로만 식을 만들었을 때 그 식을 만족하는 단 하나의 $x$를 구할 수 있습니다. 그 밑에 전부 숫자가 $0$인 부분으로만 식을 만들었을 때는 어떤 $x$를 대입해도 $0$밖에 얻을 수 없습니다.

따라서 위를 $Rx = b_1$, 아래를 $0x = b_2$라고 표현했을 때, $Rx = b_1$을 만족하는 $x$를 구하면 우리는 답을 얻게됩니다.

오차의 크기는 $\left|Ax - b\right| = \left|b_2\right|^2_2$가 되겠죠.

다시 문제로

A-1), A-2)에서 얘기한 성질을 통해, 문제를 더 간단하게 만들 수 있는 힌트를 얻었습니다.

\[Q^T A = R\]

[Q는 Orthogonal Matrix, R은 Upper Triangle Matrix] 를 만족하는 $Q$를 구하면, $Q^TA = R \rightarrow QQ^TA = QR \rightarrow A = QR$이 되고

\[Ax \cong b \rightarrow QRx \cong b \rightarrow Rx \cong Q^Tb\]

로 나타낼 수 있게 됩니다.

이제 문제가 $Rx \cong Q^Tb$ 형태가 되었는데요, 이는 A-2)에서 봤던 것처럼 아주 풀기 쉬운 형태입니다. A-1)에서 본 것처럼, $Q^T$를 $b$에 곱해도 그 크기에는 영향을 주지 않기 때문에 A-2)처럼 풀 수 있습니다.

따라서, $A = QR$이 되는 $Q, R$을 찾기만 하면 문제는 아주 쉬워집니다.

QR분해

$A$를 $QR$ QR코드 , 두개의 행렬의 곱으로 분해하는 방법을 QR decomposition(QR분해) 라고 합니다.

여기에는 몇가지 방법이 있는데, 오늘 소개해드리려고 하는건 Householder Transformation(하우스홀더변환)을 이용한 방법입니다.

하우스홀더변환

행렬 중 하우스홀더행렬이라고 불리는 행렬이 있습니다. 하우스홀더행렬은 길이가 1인 Unit Vector(단위벡터)$v$에 대해 다음과 같이 정의됩니다.

\[H = I - 2v v^T\]

이렇게 만들어진 행렬 $H$는 임의의 벡터$x$에 곱했을 때, 벡터$v$에 직교하는 평면에 대해 벡터$x$를 반전시킵니다. 따라서, $P = I - 2uu^T$일 때, 다음과 같은 그림을 그려볼 수 있습니다.

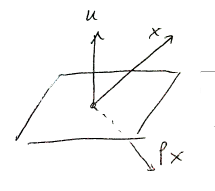
[$Px$는 $x$를 $u$와 직교하는 평면에 대해 반전시킨 결과다.]

이렇게 하우스홀더행렬은 벡터를 특정 평면에 대해 반전시킬 때 쓸 수 있습니다. 또, 하우스홀더행렬은 Orthogonal Matrix입니다.

그럼 만약 벡터$x$를 unit vector $y$의 방향으로 변환시키고 싶을 때는 어떻게 할 수 있을까요? 벡터$x$를 unit vector $y$의 방향으로 변환시키면 $\left|x\right|y$가 될테니까, 벡터$x$와 벡터$\left|y\right|$를 양분하는 평면의 normal vector(법선벡터)를 구해 $v$라고 하고, 이 벡터로 하우스홀더행렬을 구해 $x$에 곱하면 됩니다.

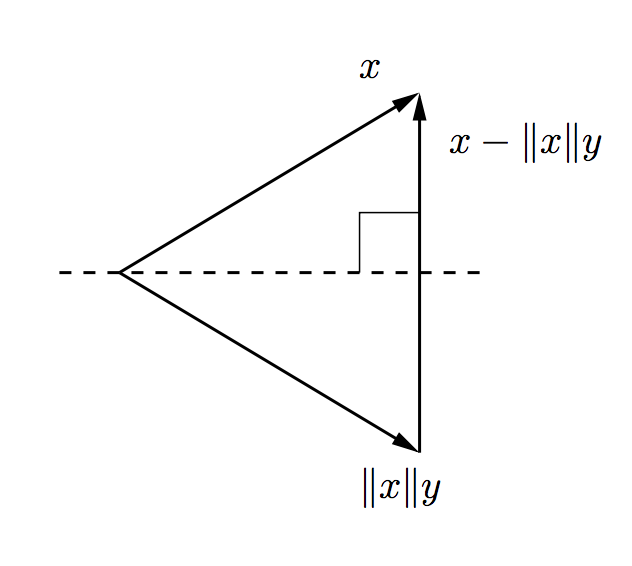
[벡터$v$ 는 $x - \left|x\right|y$의 unit vector로 둘 수 있다.$]

\[\begin{align*} (I - 2vv^T)x &= x - 2 \frac{(x + \left|x\right\|y)(x^Tx + \left\|x\right\|x^Ty)}{\left\|x\right\|^2 + 2x^Ty\left\|x\right\|^2\left\|y\right\|^2} \\ &= x - ( x - \left\|x\right\|y) \\ &= \left\|x\right\|y \end{align*}\]

[벡터$v$를 $x - \left|x\right|y$의 unit vector로 두면 $x$를 $\left|x\right|y$로 변환시킬 수 있다.]

여기서 만약 $y$가 첫번째 값이 $\pm 1$이고 나머지 값이 모두 $0$인 unit vector라면, $u = x - \left|x\right|y$라고 했을 때, $u$의 unit vector $v = \frac{u}{\left|u\right|}$라고 하고, 하우스홀더행렬 $Q_1 = I - 2vv^T$를 사용해 아래처럼

\[Q_1A = \begin{bmatrix} * & * \\ 0 & * \\ 0 & * \\ & \\ \vdots & \vdots \\ 0 & * \end{bmatrix}\]

첫번째 열을 처음빼고 전부 0인 행렬로 만들 수 있습니다. (대박)

이걸 반복해서 하면 어떻게 될까요. 그러니까 첫번째 줄은 1번째 빼고 다 0으로 만들었으니, 이번엔 첫번째 열, 첫번째 행을 제외한 나머지 부분에 대해서도 같은 계산을 해볼 수 있습니다.

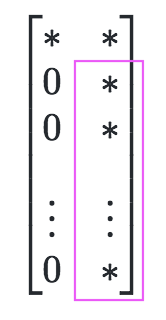
[네모로 표시한 부분]

$Q_1$과 같은 방법으로 나머지 행렬에 대한 하우스홀더행렬 $\hat{Q_2}$를 구하면 $Q_1$보다 행렬의 크기가 작을테니, $Q_2$는

\[Q_2 = \begin{bmatrix} 1 & 0 \\ 0 & \hat{Q_2} \end{bmatrix}\]

으로 정의해줍니다.

이런 $Q_1$ , $Q_2$를 $A$에 곱하면 다음과 같은 결과를 얻을 수 있습니다.

\[Q_2 Q_1 A = \begin{bmatrix} * & * \\ 0 & * \\ 0 & 0 \\ \vdots & \vdots \\ 0 & 0 \end{bmatrix}\]

[Upper Trianglular Matrix를 얻었다!]

여기서 $Q_1$ , $Q_2$은 모두 orthogonal matrix이기 때문에, $\hat{Q} = Q_2 Q_1$ 또한 orthogonal matrix입니다. $Q = \hat{Q^T}$라고 할 때, $A$를 다음과 같이 표현할 수 있습니다.

\[A = QR\]

[대박사건…]

이 과정을 파이썬으로 구현하면 다음과 같이 구현할 수 있습니다.

def qr_householder(A):
    m, n = A.shape
    Q = np.eye(m) # Orthogonal transform so far
    R = A.copy() # Transformed matrix so far

    for j in range(n):
        # Find H = I - beta*u*u' to put zeros below R[j,j]
        x = R[j:, j]
        normx = np.linalg.norm(x)
        rho = -np.sign(x[0])
        u1 = x[0] - rho * normx
        u = x / u1
        u[0] = 1
        beta = -rho * u1 / normx

        R[j:, :] = R[j:, :] - beta * np.outer(u, u).dot(R[j:, :])
        Q[:, j:] = Q[:, j:] - beta * Q[:, j:].dot(np.outer(u, u))
        
    return Q, R

[하우스홀더 변환을 이용한 QR분해 구현. 출처]

그래서 결과는 뭔가요

드디어! $A = QR$의 형태를 얻었으니 이걸 이용해 원래 풀고 싶었던 문제인 $Ax \cong b$를 풀어 배달거리에 따른 배달시간 예측모델을 만들어볼 수 있습니다!

m, n = data.shape
A = np.array([data[:,0], np.ones(m)]).T
b = data[:, 1] 

Q, R = qr_householder(A) 
b_hat = Q.T.dot(b) 

R_upper = R[:n, :]
b_upper = b_hat[:n]  

print(R_upper, b_upper) 

x = np.linalg.solve(R_upper, b_upper) 
slope, intercept = x

[파이썬 numpy를 사용해 간단하게 문제를 풀 수 있다.]

그리고 얻은 결과를 그래프로 그려볼 수 있습니다.

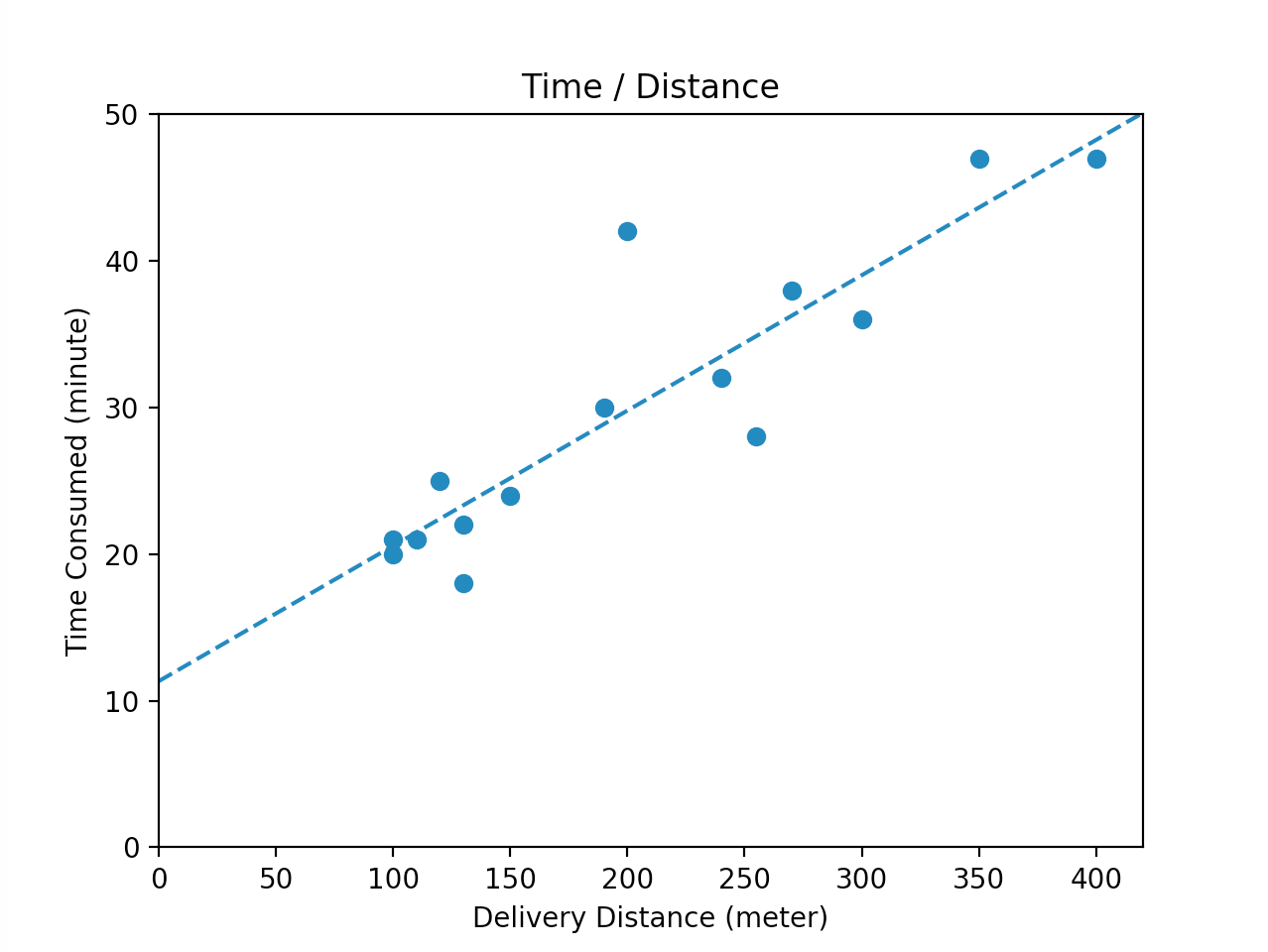
[slope: 0.092, intercept: 11.33]

[저 선 하나 그리려고 지금… ]

짠! 배달시간을 얼추 예상해볼 수 있는 모델이 생겼네요. $f(d) = 0.092d + 11.33$으로 거리 $d$에 따라 시간을 예상해볼 수 있겠습니다.

물론 실제 배달시간은 배달거리 이외에도 음식 종류, 날씨, 교통상황, 배달원이 누군지 등등, 여러 변수의 영향을 받게 되므로 실제로는 더 복잡한 방식으로 예측하고 있습니다. 하지만 이에 대해서도 유사한 방식으로 선형모델을 시도해 볼 수 있습니다.

이렇게 Linear Least Squares 문제를 파이썬으로 풀어보았습니다. 감사합니다!